Solving Runge Kutta 4th order calculator ordinary differential equations (ODEs) is one of the cornerstones of applied mathematics, engineering, and science. From predicting how a population grows to understanding how an electrical circuit behaves, ODEs provide the mathematical framework behind many real-world systems. However, solving them analytically is not always possible, especially when the equations become complex.
This is where numerical methods step in. Among them, the Runge-Kutta 4th Order Method (RK4) stands out as one of the most reliable techniques. A Runge-Kutta 4th Order Calculator takes this method and transforms it into a fast, easy, and accurate online solution. Whether you are a student working on assignments, an engineer designing systems, or a researcher simulating natural phenomena, an RK4 calculator helps you solve ODEs online in just a few clicks.
What is Runge Kutta 4th Order Method?
The Runge Kutta methods were developed in the early 20th century by Carl Runge and Wilhelm Kutta, two German mathematicians. Their goal was to provide an alternative to simpler but less accurate numerical approaches like Euler’s method.
The 4th order Runge Kutta method became the most popular version because it strikes the perfect balance between accuracy and efficiency. It uses four slope evaluations at each step to approximate the solution curve of an ODE. Compared to Euler’s method, which can drift significantly from the true solution, RK4 stays much closer to the exact value even with larger step sizes.
In short, RK4 is considered the “gold standard” in numerical methods for first-order ODEs.
Runge Kutta 4th Order Formula (Step-by-Step)
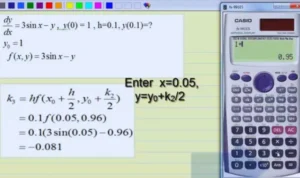
Let’s consider the general first-order ODE:
dydx=f(x,y),y(x0)=y0\frac{dy}{dx} = f(x, y), \quad y(x_0) = y_0dxdy=f(x,y),y(x0)=y0
The RK4 method approximates the next value yn+1y_{n+1}yn+1 using four slopes:
k1=h⋅f(xn,yn)k_1 = h \cdot f(x_n, y_n)k1=h⋅f(xn,yn) k2=h⋅f(xn+h2,yn+k12)k_2 = h \cdot f\left(x_n + \frac{h}{2}, y_n + \frac{k_1}{2}\right)k2=h⋅f(xn+2h,yn+2k1) k3=h⋅f(xn+h2,yn+k22)k_3 = h \cdot f\left(x_n + \frac{h}{2}, y_n + \frac{k_2}{2}\right)k3=h⋅f(xn+2h,yn+2k2) k4=h⋅f(xn+h,yn+k3)k_4 = h \cdot f(x_n + h, y_n + k_3)k4=h⋅f(xn+h,yn+k3)
Finally,
yn+1=yn+16(k1+2k2+2k3+k4)y_{n+1} = y_n + \frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4)yn+1=yn+61(k1+2k2+2k3+k4)
Here:
- hhh = step size
- f(x,y)f(x, y)f(x,y) = function defining the ODE
- yny_nyn = current value
- yn+1y_{n+1}yn+1 = next value
This weighted average of four slopes provides excellent accuracy compared to single-slope methods.
How Does a Runge Kutta 4th Order Calculator Work Online?
A Runge Kutta 4th Order Calculator simplifies the above steps and executes them automatically. Instead of doing lengthy calculations by hand, you just enter your problem’s values:
- Input: The function f(x,y)f(x, y)f(x,y), initial condition, step size, and endpoint.
- Processing: The calculator computes k1,k2,k3,k4k_1, k_2, k_3, k_4k1,k2,k3,k4 for each step.
- Output: You get the approximate solution values for yyy at chosen points.
Quick Comparison of Numerical Methods
| Method | Accuracy | Steps Needed | Best Use Case |
| Euler’s Method | Low | Few | Simple problems, quick estimates |
| Heun’s Method | Medium | Moderate | Improved accuracy over Euler |
| RK4 Method | High | More | Complex ODEs in engineering & science |
Why are RK4 calculators widely used? They provide the best trade-off between efficiency and accuracy.
Practical Example Using RK4 Calculator

Let’s solve a simple example to illustrate the power of RK4.
Problem: Solve the ODE
dydx=x+y,y(0)=1\frac{dy}{dx} = x + y, \quad y(0) = 1dxdy=x+y,y(0)=1
with step size h=0.1h = 0.1h=0.1.
Step 1: Calculate k1k_1k1:
k1=h⋅f(x0,y0)=0.1⋅(0+1)=0.1k_1 = h \cdot f(x_0, y_0) = 0.1 \cdot (0 + 1) = 0.1k1=h⋅f(x0,y0)=0.1⋅(0+1)=0.1
Step 2: Calculate k2k_2k2:
k2=h⋅f(x0+h/2,y0+k1/2)=0.1⋅(0.05+1.05)=0.110k_2 = h \cdot f(x_0 + h/2, y_0 + k_1/2) = 0.1 \cdot (0.05 + 1.05) = 0.110k2=h⋅f(x0+h/2,y0+k1/2)=0.1⋅(0.05+1.05)=0.110
Step 3: Calculate k3k_3k3:
k3=0.1⋅(0.05+1.055)=0.1105k_3 = 0.1 \cdot (0.05 + 1.055) = 0.1105k3=0.1⋅(0.05+1.055)=0.1105
Step 4: Calculate k4k_4k4:
k4=0.1⋅(0.1+1.1105)=0.12105k_4 = 0.1 \cdot (0.1 + 1.1105) = 0.12105k4=0.1⋅(0.1+1.1105)=0.12105
Final Value:
y1=y0+16(k1+2k2+2k3+k4)=1+16(0.1+0.22+0.221+0.12105)=1.11035y_1 = y_0 + \frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4) = 1 + \frac{1}{6}(0.1 + 0.22 + 0.221 + 0.12105) = 1.11035y1=y0+61(k1+2k2+2k3+k4)=1+61(0.1+0.22+0.221+0.12105)=1.11035
So after one step, y(0.1)≈1.11035y(0.1) \approx 1.11035y(0.1)≈1.11035.
Applications of Runge Kutta 4th Order Method
The RK4 method and calculators are used across disciplines:
- Engineering: Analyzing vibrations, fluid flow, and circuit dynamics.
- Physics: Modeling motion under forces, quantum simulations, and heat transfer.
- Biology: Population growth models, disease spread, and genetics.
- Economics: Forecasting, market modeling, and financial risk simulations.
- Computer Science: Algorithm design, simulations, and machine learning models.
Wherever there is change over time, RK4 finds a role.
Advantages of Using Online RK4 Calculator
- Saves time: No manual slope calculations.
- Accuracy: Produces near-exact solutions with fewer steps.
- User-friendly: Input values and get instant results.
- Educational: Many calculators provide step-by-step tables.
- Accessible: Free tools available online for students and professionals alike.
Limitations of RK4 and Calculators
While powerful, RK4 isn’t flawless:
- Step size sensitivity: Too large a step reduces accuracy; too small increases computation.
- Not for stiff ODEs: Specialized methods are needed for very stiff equations.
- Dependent on initial values: Works best with well-defined initial conditions.
Still, RK4 remains the most reliable method for a wide range of real problems.
FAQs
Q1. What is the Runge Kutta 4th Order Calculator used for?
Ans: The Runge Kutta 4th Order Calculator is designed to solve ordinary differential equations numerically. It applies the RK4 method, which is known for its balance of accuracy and efficiency. Students, engineers, and researchers use it to handle equations that are otherwise difficult to solve manually.
Q2. Is RK4 more accurate than Euler’s method?
Ans: Yes, Runge Kutta 4th order calculator is significantly more accurate than Euler’s method. While Euler’s method uses only one slope to estimate the next value, Runge Kutta 4th order calculator calculates four slopes and combines them in a weighted average. This results in solutions that are closer to the true curve of the equation.
Q3. Can I solve any ODE with this calculator?
Ans: You can solve most first-order ordinary differential equations with initial conditions using the RK4 calculator. However, certain problems, especially very stiff equations, may require more advanced numerical techniques. For regular equations, RK4 works effectively and gives reliable results.
Q4. Do engineers and researchers use RK4 calculators?
Ans: Absolutely. Engineers and scientists use Runge Kutta 4th order calculator calculators in simulations, control systems, and applied research. The method is widely adopted in physics, biology, and economics because it provides fast and accurate approximations. It bridges theoretical equations with practical real-world applications.
Q5. Is the Runge Kutta 4th order calculator free online?
Ans: Yes, many versions of the Runge Kutta 4th order calculator calculator are freely available online. Students, educators, and professionals can access them without cost, making it a highly accessible learning and problem-solving tool. Most platforms also include step-by-step instructions for better understanding.
Q6. Does RK4 guarantee exact solutions?
Ans: No, the Runge Kutta 4th order calculator method does not provide exact solutions, but it offers very close approximations. Its accuracy is often sufficient for practical applications, especially in engineering and science. For nonlinear equations, the results are still among the best available using numerical techniques.
Q7. What input do I need to use an RK4 calculator?
Ans: To use an Runge Kutta 4th order calculatorcalculator, you must provide the differential equation in the form dy/dx=f(x,y)dy/dx = f(x, y)dy/dx=f(x,y). Along with that, you need the initial condition, a chosen step size, and the endpoint of the interval. With these inputs, the calculator generates approximate solutions efficiently.
Final Thoughts

The Runge Kutta 4th Order Calculator is more than just a digital tool — it is a bridge between theory and practice. For students, it simplifies tough assignments. For engineers, it helps model real-world systems. For researchers, it speeds up complex simulations.
By combining accuracy with simplicity, this calculator turns an advanced mathematical technique into something accessible for everyone. Whether you’re studying, teaching, or solving real problems, the RK4 calculator is a reliable partner for making differential equations manageable.