Decimal to fraction Mathematics has always been about accuracy, precision, and simplicity. Among its many concepts, converting a decimal to a fraction is one of the most useful skills in everyday life, education, and professional fields. While decimals are widely used in calculators and digital systems, fractions are essential for deeper mathematical understanding, measurements, and real-world calculations.
How decimals are converted into fractions, why it matters, and how you can use a decimal-to-fraction converter to simplify your work.
The Basics of Decimals and Fractions
What is a Decimal?
A decimal is a way of representing a fraction or a part of a whole using base-10 numbers. For instance, 0.5 means five-tenths, which is equal to the fraction 1/2.
What is a Fraction?
A fraction is a number expressed in the form numerator/denominator. For example, 3/4 means three parts out of four. Fractions can be proper, improper, or mixed.
Decimals and fractions both express the same concept—parts of a whole—but in different forms.
Decimal to Fraction Conversion Quick Reference
| Decimal Number | Fraction Equivalent | Simplified Form | Example Use |
| 0.25 | 25/100 | 1/4 | Quarter of a whole |
| 0.50 | 50/100 | 1/2 | Half a pizza |
| 0.75 | 75/100 | 3/4 | Three-quarters of a cup |
| 0.20 | 20/100 | 1/5 | One-fifth of a group |
| 1.25 | 125/100 | 5/4 | Mixed fraction 1 1/4 |
How to convert fraction to decimal
To convert a fraction to a decimal, divide the numerator (top number) by the denominator (bottom number). For example, 3/4 divided gives 0.75, and 1/2 equals 0.5. This simple division process turns fractions into decimals easily.
Fractions that divide evenly result in terminating decimals, while others may produce repeating decimals like 1/3 = 0.333… Converting fractions to decimals is useful in mathematics, finance, science, and daily life for quick and accurate numerical representation.
How to convert decimal percentage into fraction
To convert a decimal percentage into a fraction, first write the percentage as a fraction over 100. For example, 75% becomes 75/100. Then, simplify it to the lowest terms, which gives 3/4.
Another example is 12.5%. Write it as 12.5/100, multiply by 10 to remove the decimal (125/1000), and simplify to 1/8. This method ensures accurate fractional results.
How to convert fraction to decimal without calculator

To convert a fraction to a decimal without a calculator, use long division. Divide the numerator by the denominator step by step. For example, dividing 5 by 8 gives 0.625. If the division ends, the decimal is terminating; if it continues repeating, it becomes a recurring decimal.
This manual method strengthens mathematical skills and provides exact results. It is especially helpful in exams, classroom learning, and real-life applications where calculators are not allowed or available.
Why Decimal to Fraction Conversion Matters
Fractions are foundational in mathematics, but decimals dominate modern calculations. Being able to switch between them bridges two essential mathematical languages. For example:
- In education, fractions help students understand division and ratios better.
- In finance, decimals dominate currency, but fractions appear in stocks and percentages.
- In engineering and construction, fractions are vital in precise measurements like inches or centimeters.
- In cooking, fractions are easier to apply when measuring ingredients.
Understanding decimals and fractions as interchangeable strengthens problem-solving skills and supports accurate results.
How to Convert Decimal to Fraction Manually
Convert decimal to fraction
- Write down the decimal (example: 0.75).
- Count decimal places (0.75 has two decimal places).
- Write as a fraction over a power of 10 (0.75 = 75/100).
- Simplify the fraction (75/100) to 3/4.
So, 0.75 = 3/4.
Step-by-Step Decimal to Fraction Examples
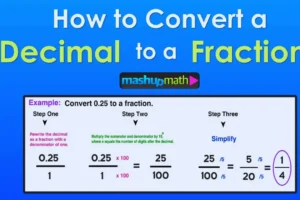
Example 1: Convert 0.25
- Decimal: 0.25
- As a fraction: 25/100
- Simplify: 1/4
Example 2: Convert 1.2
- Decimal: 1.2
- As a fraction: 12/10
- Simplify: 6/5 or 1 1/5
Example 3: Convert 0.333
- Decimal: 0.333 recurring
- As a fraction: 1/3
Example 4: Convert 2.75
- Decimal: 2.75
- As a fraction: 275/100
- Simplify: 11/4 or 2 ¾
Recurring decimal to fraction
A recurring decimal to fraction conversion is the method of expressing a repeating decimal as a fraction. For example, 0.333… becomes 1/3, and 0.666… becomes 2/3. By using algebraic techniques, repeating digits can be accurately represented as fractions. This conversion is useful in mathematics, engineering, and everyday applications where exact values are preferred over approximations provided by endless decimal repetition.
Convert recurring decimal to fraction
To convert a recurring decimal to a fraction, first represent the repeating decimal as a variable. For example, let x = 0.777… Multiply by 10 to shift digits (10x = 7.777…). Subtract the original equation (10x – x = 7), giving 9x = 7, so x = 7/9. This algebraic method works for all recurring decimals, ensuring exact fractional results.
Decimal to fraction worksheet
A decimal to fraction worksheet is a helpful practice tool that allows students to strengthen their conversion skills. It includes problems where learners change decimals like 0.25, 0.5, or 1.75 into fractions, simplify them, and sometimes express them as mixed numbers. Such worksheets are widely used in schools to improve accuracy, confidence, and understanding of decimals and fractions.
Decimal to fraction calculator
A decimal to fraction calculator is an online tool that quickly converts decimal numbers into accurate fractional equivalents. By simply entering a decimal like 0.75 or 1.2, the calculator instantly provides simplified results such as 3/4 or 6/5. It is widely used by students, teachers, and professionals for fast, error-free, and reliable mathematical conversions in daily life and academics.
Decimal to fraction chart
A decimal to fraction chart is a ready reference guide that shows common decimals and their equivalent fractions in a simplified form. For example, 0.25 = 1/4, 0.5 = 1/2, and 0.75 = 3/4. Such charts are widely used in classrooms, cooking, construction, and exams to make conversions easier, quicker, and more understandable without lengthy calculations.
Repeating decimal to fraction
A repeating decimal to fraction conversion expresses decimals with recurring digits as exact fractions. For instance, 0.333… equals 1/3, and 0.8181… equals 81/99 simplified to 9/11. Using algebraic steps or calculators, repeating patterns are turned into precise fractions. This method is essential in mathematics for accuracy, avoiding approximations, and clearly representing infinite repeating decimals in a simple fractional form.
Advantages of Using a Decimal to Fraction Converter
- Time-saving: No need for manual simplification.
- Accurate results: Eliminates calculation mistakes.
- Handles recurring decimals: Converts 0.333… or 0.666… into neat fractions.
- User-friendly: Instant results for exams, cooking, or construction.
Types of Decimal to Fraction Conversions
- Terminating Decimals:
- Example: 0.5 → 1/2
- These decimals end after a few digits.
- Example: 0.5 → 1/2
- Terminating Decimals:
- Recurring Decimals:
- Example: 0.333… → 1/3
- These decimals repeat infinitely but have fractional equivalents.
- Example: 0.333… → 1/3
- Mixed Numbers:
- Example: 2.25 → 9/4 or 2 1/4
- Converters break them into proper mixed fractions.
- Example: 2.25 → 9/4 or 2 1/4
Real-Life Applications of Decimal to Fraction Conversion
- Cooking recipes often list fractions like 1/2 cup or 3/4 spoon.
- Construction measurements use fractions for wood lengths, tiles, or fittings.
- Financial calculations like 1/8 or 3/16 appear in stock trading.
- Education and exams require students to show answers in fraction form.
FAQs
Q1. What is the easiest way to convert a decimal to a fraction?
Ans: The easiest method is to place the decimal over a power of 10 and simplify. For quick results, a decimal-to-fraction converter tool is highly recommended.
Q2. Can every decimal be converted to a fraction?
Ans: Yes, terminating and recurring decimals can always be expressed as fractions. Non-repeating, non-terminating decimals like π cannot be converted into exact fractions.
Q3. Why should I use a decimal-to-fraction converter?
Ans: A converter saves time, reduces errors, and provides exact results for recurring or complex decimals that are difficult to convert manually.
Q4. Are fractions better than decimals in mathematics?
Ans: Neither is better; both are essential. Fractions are more intuitive in divisions and ratios, while decimals are preferred for digital precision and currency.
Q5. Can mixed decimals like 2.75 be converted into fractions?
Ans: Yes, mixed decimals can be expressed as improper fractions or mixed fractions. For example, 2.75 = 11/4 = 2 3/4.
Final Thoughts
Converting decimals to fractions is a valuable skill for math, education, and daily tasks. With practice or a converter, you can simplify numbers quickly, improve accuracy, and confidently handle multiple formats for real-life and professional calculations.